宇宙の交響曲:創造の言語としての黄金比、フィボナッチ数列、フラクタルの形而上学的考察
第一部:聖なる三位一体 ― 宇宙の数学的構造を解き明かす
宇宙が自らを表現するために用いる言語が存在するとすれば、それは数字と幾何学の語彙で綴られているのかもしれません。その中でも、黄金比、フィボナッチ数列、そしてフラクタルという三つの概念は、単なる数学的な抽象論を超え、万物の形態と成長を司る根源的な設計原理として浮かび上がります。これらは互いに深く結びつき、宇宙の展開を支配する動的な三位一体を形成しているのです。
1.1 黄金比(Φ):神聖なる比率の署名
黄金比、ギリシャ文字の$\Phi$(ファイ)で表されるこの比率は、古来より人間の美的感覚と深く共鳴してきました。その数学的定義は、一本の線を大小二つの部分に分割する際に、「全体と大きい部分の比」が「大きい部分と小さい部分の比」と等しくなる、唯一無二の分割法です 。この比率は約
1:1.618となり、無理数として無限に続きます。
**「全体の長さに対して、大きい部分の比率が小さい部分に対しても同じ比率になる」**という特別な比率のことです。
その歴史は古く、紀元前300年頃の数学者ユークリッドの著作『原論』にまで遡ることができますが、当時はまだ「黄金比」とは呼ばれていませんでした 。この比率が神聖な意味合いを帯びるのは、ルネサンス期に数学者ルカ・パチョーリがレオナルド・ダ・ヴィンチの挿絵を伴って出版した『神聖比例論』において、「神の比率」として称揚されてからのことです 。この歴史的背景は、黄金比が単なる数値ではなく、古くから神聖さ、完全性、そして調和の象徴と見なされてきたことを示しています 。また、五芒星のような神秘主義的な意味合いを持つ図形の内部にも、この比率は繰り返し現れます 。
しかし、黄金比の真のスピリチュアルな意義は、その数値自体にあるのではありません。それは、この比率が体現する「関係性の原理」と「共鳴の法則」にこそあります。黄金比の定義((a+b)/a=a/b)は、本質的に部分と全体の関係性について語っています。それは、部分と全体が再帰的かつ美しい絆で分かちがたく結ばれている、完璧な自己言及的調和の原型なのです。スピリチュアルな探求において、「関係性」は核となる概念です――自己と他者、自己と神、ミクロコスモスとマクロコスモスの関係性。したがって、黄金比は、あらゆる部分が全体の美を反映し、全体がその部分において完璧に表現されるという、調和のとれた関係性の数学的定式化と解釈することができます。それは、数によって表現された非二元性(ノンデュアリティ)の署名なのです。
1.2 フィボナッチ数列:生命の生成的リズム
フィボナッチ数列は、0, 1, 1, 2, 3, 5, 8, 13, 21…と続く、一見単純な数の連なりです。その生成規則は極めて明快で、各項が直前の二つの項の和に等しい(Fn=Fn−1+Fn−2)というものです 。この数列は、13世紀の数学者レオナルド・フィボナッチ(ピサのレオナルド)が「兎のつがいの増え方」という問題を通じて紹介したことで知られ、その起源からして生物の有機的な成長や増殖をモデル化する性質を内包しています 。
この数列の最も驚くべき特性は、数列が進むにつれて、隣り合う二つの項の比が黄金比(約1.618)に限りなく収束していく点にあります 。この収束こそが、成長のプロセス(フィボナッチ)と完璧な比率の原理(黄金比)とを分かちがたく結びつける数学的な架け橋です。
表1:フィボナッチ数列の隣接項の比と黄金比(Φ)への収束
| Fn | Fn+1 | 比率 (Fn+1/Fn) |
| 1 | 1 | 1.000000 |
| 1 | 2 | 2.000000 |
| 2 | 3 | 1.500000 |
| 3 | 5 | 1.666667 |
| 5 | 8 | 1.600000 |
| 8 | 13 | 1.625000 |
| 13 | 21 | 1.615385 |
| 21 | 34 | 1.619048 |
| 34 | 55 | 1.617647 |
| 55 | 89 | 1.618182 |
| 89 | 144 | 1.617978 |
| 144 | 233 | 1.618056 |
| 233 | 377 | 1.618026 |
| 377 | 610 | 1.618037 |
| 610 | 987 | 1.618033 |
| 987 | 1597 | 1.618034 |
この表が示すように、比率は黄金比の値を挟んで振動しながら、急速にその値に近づいていきます。この数学的事実は、単なる計算結果以上の深い意味を物語っています。それは、宇宙における生命の成長プロセスが、無秩序に進行するのではなく、常に理想的な調和の状態(黄金比)へと向かう、ある種の「傾向」や「意志」を持っていることを示唆しているのです。
1.3 フラクタル:無限の反映という原理
フラクタルは、その核心的な特徴である「自己相似性」によって定義される幾何学的な概念です。これは、図形の一部を拡大すると、図形全体と非常によく似た形が現れる性質を指します 。マンデルブロ集合のような数学的に完璧なフラクタルは自然界には存在しませんが、自己相似性の「原理」は、海岸線や山脈の形状、雲の輪郭、川の分岐、稲妻の閃光、そして樹木やシダ、血管網といった生物の構造など、森羅万象に見出すことができます 。フラクタルは、単純な規則の繰り返しから、いかにして複雑な構造がスケールを超えて生み出されるかを説明する、宇宙の幾何学的な法則なのです。
これら三つの概念を統合すると、単に関連性があるというだけでなく、一つの首尾一貫した、形而上学的な創造のエンジンを形成していることが明らかになります。
- フィボナッチ数列は、成長の「衝動」あるいは「プロセス」そのものです。それは一歩一歩、段階的に展開していくダイナミックな力です。
- 黄金比は、その成長が最適な調和と効率性を保つために従う「法則」あるいは「導きの原理」です。成長はランダムではなく、この普遍的な比率に導かれています。
- フラクタルは、この導かれたプロセスが、あらゆるスケールで自己を繰り返し、その結果として現れる「構造」あるいは「顕現した姿」です。
この三位一体は、スピリチュアルな観点から、創造のプロセスをエレガントに説明するモデルを提供します。すなわち、「神聖なる成長への衝動(フィボナッチ)」が、「神聖なる調和の法則(黄金比)」に従って作用し、その結果として「神聖なる現実の顕現(フラクタル)」がもたらされるのです。そこでは、あらゆる部分が全体を反映し、宇宙は無限の入れ子構造としてその姿を現します。
第二部:生ける設計図 ― 顕現における諸原理の観察
この「聖なる三位一体」は、理論的な好奇心の対象に留まりません。それは、私たちが住む物理的世界の、生きて呼吸する設計図そのものです。ここでは、抽象的な原理から具体的な顕現へと視点を移し、これらの法則が自然界や人類の創造物の中でいかに息づいているかを探ります。
2.1 生命の展開:植物界と動物界のパターン
生命が自らを形作る際、これらの数学的原理は驚くほど頻繁に現れます。植物界では、多くの花の花弁の数が3枚、5枚、8枚、13枚といったフィボナッチ数になることが知られています 。ヒマワリの種の配列や松ぼっくりの鱗片は、互いに逆向きの二重螺旋を描いており、それぞれの螺旋の数が34と55のような隣り合うフィボナッチ数になることが多く見られます 。これらのパターンは単なる偶然ではなく、限られたスペースに種子を最も効率的に配置し、太陽光を最大限に浴びるための、進化の過程で獲得された最適な生存戦略なのです 。樹木の枝分かれもまた、フィボナッチ数列に従うことで、葉が重なり合うのを最小限に抑え、光合成の効率を高めています 。
動物界においても、巻貝の殻や動物の角の成長は、美しい対数螺旋を描きます 。ここで、一般に流布している「オウムガイの殻は完璧な黄金螺旋である」という説には、注意が必要です。科学的な計測によれば、オウムガイの螺旋は自己相似的な成長を示す見事な対数螺旋(生命の曲線)ではあるものの、その比率は厳密には黄金比とは異なります 。さらに、生命の設計図であるDNAの二重螺旋構造にも、その一周期における長さの比率に黄金比との関連性が指摘されています 。
オウムガイの例のように、自然界の多くの形態が、これらの比率の「近似値」であって、数学的に完璧な表現ではないという事実は、そのスピリチュアルな意義を何ら損なうものではありません。宇宙は厳格なコンピュータ・シミュレーションではないのです。スピリチュアルな真理は、生命の表現方法として、螺旋、分岐、調和のとれた比率といった「元型的なパターン」が、否定しようのないほど広く採用されているという事実にあります。生命は、このエレガントな効率性を目指して「努力」しているように見えます。これらの数学的理想(黄金比やフィボナッチ数列)は、生命の形態形成場における強力なアトラクター(引き寄せるもの)として機能しているのかもしれません。私たちがこの普遍的な傾向を認識することこそが、そのスピリチュアルな意味の源泉なのです。
2.2 人類の創造物における反響:芸術、建築、そして調和への探求
人類もまた、意識的あるいは無意識的に、これらの宇宙的な原理を自らの創造物の中に反映させてきました。古代エジプトのギザの大ピラミッドや古代ギリシャのパルテノン神殿といった歴史的建造物には、その設計に黄金比が用いられていると広く考えられています 。ルネサンス期には、レオナルド・ダ・ヴィンチが『モナ・リザ』の構図や『ウィトルウィウス的人体図』において、この比率を応用したとされています 。
ただし、これらの歴史的な応用が常に意識的かつ厳密な計算に基づいていたかについては、学術的な議論があり、一部では「都市伝説」の類いと見なす向きもあります 。しかし、重要なのは、その意図が意識的であったか直感的であったかにかかわらず、これらの比率が結果として、時代や文化を超えて人々に「美しい」「調和がとれている」という感覚を呼び起こしてきたという事実です 。
この事実は、人間の創造的精神が、神聖さや美を追求する際に、宇宙が自己を組織化するために用いるのと同じ根源的な比率と自然に共鳴し、それを再発見することを示唆しています。古代の建築家が神殿を建てる時、彼らは神との繋がりを求めていました。その過程で彼らがたどり着いた比率が、宇宙の調和の比率と一致するのは、人間の創造行為が、宇宙の秩序への積極的な参加形態であるからに他なりません。芸術や建築は、人間界と神聖な領域との間に、共通の幾何学的言語を用いて架け橋を築こうとする、スピリチュアルな実践となるのです。
2.3 壮大なるデザイン:DNAの螺旋から銀河の渦まで
これらのパターンの最も深遠な特徴の一つは、フラクタル幾何学の真骨頂である、そのスケール不変性です。巻貝の成長を支配する対数螺旋は、はるか宇宙の彼方で渦巻く銀河の腕や、地球上で発生する台風の雲の渦にも、同じ形として現れます 。一本の樹木の枝分かれのパターンは、川が三角州を形成する様子、空を切り裂く稲妻、そして私たちの肺の気管支の分岐構造にまで反響しています 。
この事実は、生物学的なミクロの世界から、気象学的な現象、そして宇宙論的なマクロの世界に至るまで、全く異なるスケールと物理法則の下で、同じ根源的な形成原理が働いていることを示しています。これは、宇宙が互いに無関係な物体や法則の寄せ集めではなく、単一の、統一された、首尾一貫したシステムであることを強く示唆します。宇宙は、量子のレベルから宇宙のレベルまで再帰的に適用される、ごく少数の単純な生成原理に基づいて動いているのです。
形而上学的な観点から見れば、これは宇宙が、単一の根源的な意識あるいは知性の顕現であることを意味します。その意識は、自己言及的で一貫した形態の言語――すなわち神聖幾何学の言語――を通じて、自らを表現しているのです。スケールを超えてパターンが繰り返されるという事実は、宇宙が単に思考のように「構造化されている」のではなく、宇宙そのものが、あらゆる拡大レベルにおいて自身の本性を無限に映し出す、一つの「思考」である可能性を示唆しています。
第三部:スピリチュアルな統合 ― 宇宙の言語を解釈する
数学的な観察と物理的な証拠を統合し、私たちは今、これらの原理が持つより深いスピリチュアルな意味を探求する段階に至ります。なぜ宇宙はこのような構造を持つのか、そしてその中で生きる私たちにとって、それは何を意味するのか。ここでは、その核心に迫ります。
3.1 神聖幾何学:形而上学的な枠組み
神聖幾何学とは、これらの数学的パターンを、単なる物理現象の記述ではなく、万物の存在の基盤そのものであると理解する、哲学的・スピリチュアルな枠組みです 。この思想は、宇宙が単一の意識の点から、特定の幾何学的な形態と比率を通じて展開していくと説きます。これは、「万物は数なり」と述べた古代ギリシャの哲学者ピタゴラスの思想にも通じます 。黄金比、フィボナッチ数列、フラクタルは、「神聖なる幾何学者」が用いる道具箱の主要なツールなのです。フラワー・オブ・ライフのような、これらの原理に基づいて構築された図形は、原子から銀河に至るまでのあらゆるもののパターンを内包する、創造の青写真と見なされています 。
この観点から見ると、数字や比率は静的な量ではなく、特定の「振動周波数」あるいはエネルギーのパターンを表すものと解釈できます。古代ピタゴラス学派が数と音楽的調和、そして宇宙の秩序を結びつけたように、現代物理学もまた、万物の根源がエネルギーと振動であることを理解しています 。この二つの考えを繋ぎ合わせることで、私たちが観察する数学的法則は、宇宙の根源的な周波数の形式的な記述であると考えることができます。フィボナッチ数列は展開するエネルギーのリズムであり、黄金比は調和と生命そのものの周波数です。マンダラアートを描いたり、自然の造形を瞑想的に観察したりすることを通じて神聖幾何学に触れることは、私たち自身の意識を、これらの宇宙的で生命を肯定する周波数に同調させる行為(チューニング)なのです 。
3.2 意識の共鳴:なぜ私たちは美と秩序を知覚するのか
根源的な問いがここにあります。なぜ私たちは、これらのパターンを「美しい」と感じるのでしょうか?その答えは「共鳴」という言葉に集約されます。私たちの美的感覚は、単なる文化的な構築物ではなく、生物学的かつスピリチュアルな要請に基づいているのです。私たちの身体は、手足の比率からDNAの螺旋構造に至るまで、自然界を形作るのと同じ原理に基づいて構築されています 。
したがって、私たちが自然の中や芸術作品の中に黄金比やフィボナッチ螺旋を内包した形を知覚する時、私たちの意識は、実質的に「自己」を認識しているのです。私たちの内なる構造と、外なる世界との間で生じるこの認識行為が、「美」や「調和」と呼ぶ感覚を生み出します 。実際に、fMRIを用いた脳科学の研究では、黄金比に近い比率の図形を見たときに、脳の特定の部位が異なる活動を示すことが示唆されており、この好みが神経学的な基盤を持つ可能性を示しています 。
ここから導き出されるのは、美という感覚が単なる快楽ではなく、私たちを生命肯定的で、調和がとれ、宇宙の秩序と一致するものへと導く「スピリチュアルな羅針盤」として機能しているという考えです。それは、私たちが現実の真の姿を反映するものと出会った時に、より深い自己から送られてくる直感的な合図なのです。生存に有利なもの(健康な伴侶や豊かな土地など)に魅力を感じるという生物学的な本能が、スピリチュアルなレベルにまで拡張されたものと言えるでしょう。私たちは、生命、調和、そして神聖な知性のエッセンスそのものを表すこれらのパターンに惹きつけられるのです。美の感覚に従うことで、私たちは無意識のうちに、宇宙の創造的で秩序ある原理と自らを調和させようとしているのです。
3.3 フラクタルな意識と相互接続された自己
この統合の旅がたどり着く最も深遠なスピリチュアルな含意は、「宇宙がフラクタルであるならば、私たち自身もまたフラクタルである」という認識です。これは、古代の秘教的原理である「上なるものは下なるものの如く、下なるものは上なるものの如し」という言葉に集約されています 。この言葉は、数学的な自己相似性の概念を、古くから言い表したものです。
人間は宇宙の中に存在する孤立した存在ではなく、マクロコスモス(大宇宙)の全体像をその構造の中に内包するミクロコスモス(小宇宙)なのです 。私たちの血管系や神経系がフラクタルなネットワークを形成しているように、私たちの物理的な身体はこの原理を反映しています 。
このフラクタルな自己相似性の原理は、物理的な身体を超え、意識そのもののレベルにまで及びます。個々の魂や意識の点は、宇宙意識の単なる「断片」ではなく、その「完全なホログラフィックな投影」です。つまり、私たち一人ひとりの中に、宇宙全体のパターンが内包されているのです。この理解は、分離という幻想を打ち砕き、深遠なスピリチュアルな真理の基盤を形成します。それは、瞑想や内省を通じて自己の深くに入ることで、宇宙全体の叡智にアクセスできる可能性を示唆します。直感(部分が全体の知識にアクセスする能力)のメカニズムを説明し、「神の国は汝らの内にあり」という教えに具体的な根拠を与えます。それは、すべての個人が神聖であり、その内に神性を丸ごと含んでいることを意味します。これこそが、フラクタルな現実がもたらす、究極のスピリチュアルな帰結なのです。
第四部:結論 ― 宇宙の秩序との調和の中で生きる
本稿で探求してきた黄金比、フィボナッチ数列、そしてフラクタルは、単なる知的な好奇心の対象ではありません。それらは、宇宙に内在する知性、調和、そして美が、目に見え、触れることのできる形で現れたものです。フィボナッチ数列という「成長のプロセス」は、黄金比という「調和の法則」に導かれ、フラクタルという「自己相似的な構造」として、あらゆるスケールで現実を織りなしています。
これらの原理は、私たちが神聖で秩序だった宇宙の中に生きており、銀河を形作り、ヒマワリを育むのと同じ法則が、私たち自身をも形作っているという事実を、絶えず思い出させてくれます。
最終的なメッセージは、読者の皆様への一つの誘いです。このレンズを通して世界を眺めてみてください。一枚の花びらの曲線に、一本の樹木の枝分かれに、そしてご自身の存在の構造そのものに、神聖なる設計図を見出すことです。そうすることで、私たちは宇宙の交響曲とより意識的に調和し、その壮大な音楽の一部として、自らの人生を奏でることができるようになるでしょう。
黄金比について
1. ユークリッド(紀元前300年頃)
- 『原論(Elements)』の第6巻において、黄金比を 「線分を極端中項比に分ける」 と定義しました。
- つまり「全体 : 大部分 = 大部分 : 小部分」という幾何学的関係式です。
- 当時は「数式」ではなく、図形と比の言葉で表されていました。
2. 代数学的な表現(中世以降)
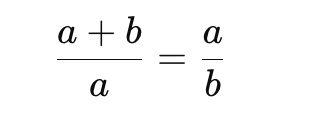
- 中世の数学者たちが、この幾何学的定義を方程式に書き直しました。
- 「線分を a(大)と b(小)に分けたとき」 上記の式を立て、それを解くことで二次方程式が得られます。
3. 近代(16〜17世紀)
- ルネサンス期の数学者たちが、代数を発展させていく過程で黄金比も方程式として扱われました。
- 特に、二次方程式 x2−x−1=0x^2 – x – 1 = 0 の解として、黄金比(φ)が得られることが明確にされました。
4. 「φ = (1+√5)/2」の形が定着したのは?
- この明確な「平方根を含む数式」としての表記は 17世紀以降の代数学の発展期 に定着しました。
- 誰か一人の発明というよりは、ユークリッドの幾何学的定義 → 代数学の進歩 → 二次方程式の解、という流れで自然にこの形に落ち着いたと言えます。
- 19世紀になるとドイツの数学者 マルティン・オーム が「goldener Schnitt(黄金分割)」という名前を使い始め、数式と名称が結びついて広まりました。
✅ 結論:
- 定義を与えたのはユークリッド(紀元前300年頃、幾何学的)
- 現代的な数式((1+√5)/2)にしたのは、17世紀以降の代数学の発展による自然な帰結
- 名前を定着させたのは19世紀のマルティン・オーム
ご希望なら、**ユークリッドの定義から「φ = (1+√5)/2」が導かれる手順(方程式の解き方)**を、図と数式でステップ解説しましょうか?
